New Integrated Govt. School Class 10 Physical Science Behaviour of gases Notes.

 

Class-10-physical-science-behaviour-of-gases-notes

                                                                                            Copyright-free image source: https://pixabay.com/

1) What is gas pressure?

Ans〉The Pressure of a gas is defined as the normal force per unit area exerted by the gas molecules on the wall of the container.

let the area of the inner surface of a container = A

and force on that surface = F

then the pressure of the gas, P = F / A

2) What instrument is used to measure the pressure of a gas?

Ans〉Manometer

3) What is atmospheric pressure?

Ans〉Atmospheric pressure: The atmospheric pressure is defined as the normal force per unit area exerted by the air molecules.

4) What instrument is used to measure the atmospheric pressure?

Ans〉Barometer

5) Write the C.G.S and S.I units of pressure. What is the relationship between them?

Ans〉The C.G.S unit of pressure = dyn / `cm^2`

           The S.I unit of pressure =  N / `m^2` or Pa (pascal)

1 Pa = 1 N / `m^2` = `\frac{1\ N}{1\ m^2}=\frac{10^5dyn}{(100)^2 cm^2}` =10 dyn / `cm^2`

∴ 1 N / `m^2` = 10 dyn / `cm^2` বা     1 dyn / `cm^2` = `10^-1` N / `m^2` 

Other units of pressure are torr, bar, PSI (pound per square inch).

1 torr = 1 mm Hg

1 bar = `10^{5}` Pa = `10^{6}` dyn / `cm^2` 

6) What do you mean by 1 atm? What is its value?

Ans〉1 atm is defined as the pressure exerted by 76 cm of mercury column at `0^\circ`.

1 atm = 76 cm Hg = 760 mm Hg 

         = 760 torr [ ∴  1 torr = 1 mm Hg]

         = 76 `\times` 13.6 `\times` 980 dyn / `cm^2`

         =  1.013 `\times` `10^6` dyn / `cm^2`

= 1.013 `\times` `10^5` Pa  [ ∴ 1 Pa = 10 dyn / `cm^2`] 

         = 1.013 bar [  ∴ 1 bar = `10^5` Pa]

         = 1013 `\times`  `10^{-3}` bar

         = 1013 milibar [ ∴ 1 milibar = `10^{-3}` bar]

7) What do you mean by 1 Pa pressure?

Ans〉1 Pa pressure: The amount of pressure created when one Newton force is applied per 1 square meter area, is called Pascal.

1 Pa = `\frac{1\ N}{1\ m^2}`

8) What are units of volume? What is the relationship between them?

Ans〉The C.G.S unit of volume = `cm^3`

The S.I unit of volume = `m^3`

1 `m^3` = `(100 cm)^3` = `10^6 cm^3`

Other units of volume are liters (L), milliliters (mL), cubic decimetres (`dm ^ 3`).

1 L = 1 `dm^3` = `10^3` `cm^3` = `10^3` mL

1 `m^3` = `10^6` `cm^3` = `10^3` `dm^3` = `10^3` L

9) Write down Boyle's law and explain it.

Ans〉Boyle's law: At constant temperature, the volume of a fixed mass gas is inversely proportional to the pressure of the gas.

Mathematical form: Suppose the volume and pressure of a certain mass of a gas at a given temperature is V and P.

ஃ according to Boyle's law,

V ∝ `\ frac1P` [when the mass and temperature of the gas are fixed]

Or V = `\ frac KP` [Here K is a constant]

Or PV = K

Now at a constant temperature, if the volume a certain mass of a gas is `V_1` at pressure `P_1` and `V_2` at pressure `P_2`, then according to Boyle's formula,

                                  `P_1V_1` = `P_2V_2`

10) What are the constants of Boyle's law?

Ans〉The constants of Boyle's law are temperature and mass of the gas.

11) Who developed an air pump to experimentally verify Boyle's law?

Ans〉Robert Boyle's assistant Robert Hooke.

12) Draw the 1) P vs V and V vs P 2) PV vs P and PV vs V 3) V vs`\ frac1P` and P vs`\ frac1V` curve according to Boyle's law

Ans〉 1) P vs V or V vs P curve: A rectangular hyperbola is obtained by plotting V along the X-axis and pressure P along the Y-axis. This graph is called isotherm or isothermal curve.

 

Note in this context that the P vs V graph is similar to the V vs P graph at a constant temperature.

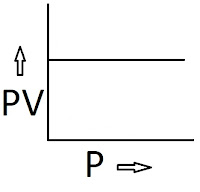
2) PV vs P and PV vs V curve: The graph will be a straight line parallel to the P-axis if we plot P along the X-axis and PV along the Y-axis.

The graph will be a straight line parallel to the V-axis if we plot V along the X-axis and PV along the Y-axis.

 3) V vs`\ frac1P` and P vs`\ frac1V` curve: The graph will be a straight line passing through the origin

                                       

13) When a balloon is inflated, both its volume and the pressure increase. Is Boyle's law violated?

Ans〉According to Boyle's law at a constant temperature, the volume of a fixed mass gas is inversely proportional to the pressure of the gas. But when the balloon is inflated, the mass of the gas increases, so Boyle's law is not applicable here. So there is no question of its violation.

14) If a bubble of air rises from the bottom of deep water, what is the reason for its increasing volume?

Ans〉As the air bubble rises from the bottom of the water, the pressure of the water decreases gradually. Let us suppose that the temperature of the water is uniform everywhere. Now according to Boyle's law, the volume and pressure of a certain mass of gas at constant temperature are inversely proportional to each other. So as the pressure on the bubble gradually decreases, its volume gradually increases.

15) Why does the size of a `H_2` gas-filled balloon increase with increasing height?

Ans〉The atmospheric pressure decreases with increasing height. Now according to Boyle's law, the volume and pressure of a certain mass of gas at constant temperature are inversely proportional to each other. The higher a balloon rises, the lower is the pressure. As a result the volume of the balloon increases.

16) Determine the relationship between pressure and density of a gas at a constant temperature.

Ans〉Let V, P, and d are the volume, pressure, and density of 'm' gram gas. 

According to Boyle's formula PV = k (constant) [when the mass and temperature of the gas are fixed]

Now, density (d) = `\frac mV`

ஃ PV = k or,  P `\times` `\frac md` = k    or   `\frac Pd` = `\frac km`

ஃ `\frac Pd` =  constant  or    P  ∝ d

Thus at a constant temperature, the pressure of a fixed mass of gas is proportional to the density of the gas.

17) write down Charle's law and explain it.

Ans〉Charle's law: At constant pressure the volume of a fixed mass of gas increases or decreases by `\frac1{273}` part of its volume at 0℃ for every 1℃ rise or fall in temperature.

Explanation: Let the volume of a fixed mass of gas at  0℃ is `V_0` and at t℃ is `V_t`.

According to Charles law,

Increase in volume due to1℃ rise in temperature 

                                                    = `\frac{V_0}{273}`

Increase in volume due to t℃ rise in temperature 

                                                    = `\frac{V_0t}{273}`

ஃ The volume of the gas at t℃ 

                                       `V_t` = `V_0+\frac{V_0t}{273}`

                                   or `V_t` = `V_0` `\left(1+\frac t{273}\right)`

This is the mathematical form of Charles's law.

Similarly, keeping the pressure constant, if the temperature is decreased by t℃, the volume of the gas becomes 

               `V_-t` = `V_0` `\left(1-\frac t{273}\right)`

18) What are the two constants of Charls's law?

Ans〉The two constants of this law are 1) mass of gas and 2) pressure of gas.

19) Why is the term 'fixed mass of a gas' mentioned while stating Boyle's and Charles' law?

Ans〉The volume and pressure of a gas depend on the mass of the gas. When the mass of a gas is changed, pressure and volume also get changed. That is why the term 'fixed mass of a gas' is always mentioned while stating Boyle's and Charles law.

20) Why is it necessary to specify the pressure and temperature of a gas when referring to its volume?

Ans〉The volume of a given mass of a gas depends on both the pressure and temperature of the gas. The volume of a gas changes when any one or both of them changes. That is why it is necessary to specify the pressure and temperature of a gas when referring to its volume.

21) Calculate the value of absolute zero temperature from Charles law.

Ans〉Let at constant pressure, the volume of a fixed mass of gas at 0℃ be `V_0` and at t℃ be `V_t`.

ஃ According to Charles' law,`V_t` = `V_0` `\left(1+\frac t{273}\right)`

Hence at t = -273 ℃, the volume of the gas becomes

`V_-273`= `V_0` `\left(1+\frac{-273}{273}\right)` = 0

Therefore according to Charles' law, at constant pressure, the volume of a gas becomes zero. That is why this temperature is called absolute zero temperature.

22) What do you mean by absolute zero temperature? What is its value?

Ans〉Absolute zero temperature: According to Charle's law, the temperature at which the volume of a certain mass of gas becomes zero at constant pressure is called absolute zero temperature.

≻ The value of absolute zero temperature is (-273℃). If accurately measured, the value of absolute zero temperature is (-273.15 ℃).

23) Why is absolute zero temperature called absolute?

Ans〉The value of absolute zero temperature 1) does not depend on the nature, quantity, initial pressure and volume of the gas. 2) The volume of a fixed mass of gas at constant pressure becomes zero at absolute zero temperature. 3) It is not possible to find less temperature than absolute zero temperature  in the universe. For these reasons, absolute zero temperature is called absolute.

24) What do you mean by absolute scale of temperature? Why is it called Kelvin scale?

Ans〉Absolute scale of temperature: The scale of temperature whose zero point is taken as -273℃ and its 1° reading is equal to 1℃ is called absolute scale of temperature.

≻Physicist Lord Kelvin introduced the concept of absolute scale of temperature.That is why this scale is called Kelvin scale after its name. 

25) Which one of the Kelvin scale and Celsius scale of temperature is more fundamental and why?

Ans〉The Kelvin scale of temperature is more fundamental. This is because the zero value of the Celsius scale depends on the physical state of a substance (melting point of pure ice or freezing point of pure water). But the zero value of the Kelvin scale is the lowest temperature in the universe. This value does not depend on the nature, mass, pressure, volume or other physical condition of the material. So it is more basic.

26) What is the relationship between temperature of Celsius and Kelvin scale?

Ans〉If the temperature of an object is t℃ on the Celsius scale and T K on the Kelvin scale, then T = t + 273

Thus, absolute scale temperature = Celsius scale temperature + 273

27) Write the alternative form of Charle's law according to the absolute scale of temperature.

Or, Write Charles' law according to the absolute scale of temperature.

Or, show that the volume of a gas at constant pressure is proportional to its absolute temperature.

Ans〉Let at constant pressure, the volume of a fixed mass of gas at 0℃ be `V_0` and at t℃ be `V_t`.

ஃ According to Charles' law,

              `V_t` = `V_0` `\left(1+\frac t{273}\right)`

                        =`V_0` `(\frac{t+273}{273})`

                        =`\frac{V_0T}{273}` [ T = t + 273 ]

Now the volume of a fixed mass of gas at 0 ℃ `V_0` is fixed

Therefore,`\frac{V_0}{273}` = constant

Therefore, V = constant X T  or, V∝ T

That is, at constant pressure the volume of a fixed mass of gas  is proportional to its absolute temperature.

This is Charles' law for the absolute scale of temperature.

28) Draw 1) V vs t (℃) and 2) V vs T (K) graphs of fixed mass gas at constant pressure.

Ans〉1) V vs t (℃)  graph:

In the case of a gas of a certain mass at constant pressure, the V vs t (℃) graph will be a straight line.

2)  V vs T graph: In case of a gas of fixed mass under constant pressure, the V vs T graph will be a straight line passing through the origin.

29) Establish the combined form of the Boyle and Charles formula.

Ans〉Suppose P, V and T are the pressure, volume and absolute temperature of a fixed mass of gas respectively.

According to Boyle's law, V ∝ `\frac1P` ( m, T constant)

According to Charles' law, V∝ T ( m, P constant)

By the rule of joint variation, V ∝  `\frac PV` (when all parameters vary)

Or, V = K `\frac PV` ( K = proportionality constant)

Or, `\frac {PV}T` = K--------(1)

Let at `T_1` K temperature, volume and pressure of a fixed mass of gas are `V_1` ＆`P_1` and at `T_2` K temperature these are `V_2` ＆`P_2` respectively.

Then from equation (1), we get

`\frac{P_1V_1}{T_1}` = K  and   `\frac{P_2V_2}{T_2}` = K

ஃ `\frac{P_1V_1}{T_1}` = `\frac{P_2V_2}{T_2}`      

30) What is ideal gas and real gas? Give examples.

Ans〉Ideal gas: Gases that obey Boyle and Charles' law are called ideal gas.

Example: Practically there is no ideal gas.

Real gas: Gases that do not follow Boyle and Charles' law are called real gas.

Example: O₂, H₂, CO₂, H₂, N_2, etc.31) Under what conditions, a real gas behaves like an ideal gas?

Ans〉At very low pressures and temperatures, real gas behaves like an ideal gas.

32) What is molar volume? What is its value?

Ans〉Molar volume: The volume occupied by 1 mole of any gas at a fixed temperature and pressure is called the molar volume of that gas.

≻ The value of molar volume at standard temperature and pressure is 

22.4 L / atm.

33) Write down and explain Explain Avogadro's law.

Ans〉Avogadro's law: At the same condition of pressure and temperature equal volume of all gases contain equal number of molecules.

Or, The volume of a gas at constant temperature and pressure is proportional to the number of moles of the gas.

Explanation: Let V is the volume of n mole gas at constant pressure and temperature.

ஃ According to Avogadro's law,

   V ∝ n or V = Kn, where K = constant. The value of K depends on the pressure and temperature of the gas.

34) Why moist air is lighter than dry air?

Ans〉The main constituents of dry air are `O_2` and `N_2`. But the main constituents of moist air are `O_2`, `N_2` and water vapour.

Now molecular weight of `O_2` = (16`times`2) = 32 

ஃVapor density of `O_2` = 32/2 = 16

Molecular weight of `N_2` = (14`times`2) = 28 

ஃ Vapor density of `N_2` = 28/2 = 14

Molecular weight of water vapour = (2`times`1 +16) = 18 

ஃVapor density of water vapor = 18/2 = 9

The vapor density of water vapour is less than that of `O_2` and `N_2`. Thus water vapor is lighter than same volume of `O_2` and `N_2`. So moist air is lighter than dry air.

35) Establish the ideal gas equation formed by combining Boyle's law, Charles' law and Avogadro's hypothesis.

Or, In the case of n mole of gas, establish the ideal gas equation PV = nRT.

Ans〉Let at T K temperature and P atm pressure, the volume of n-gram mole of gas is V lit. Then

from Boyles law, V ∝ `\frac1P` ( n, T constant)

from Charles' law, V∝ T (n, P constant) and

from Avogadro's law, V∝ n (P, T constant)

By the rule of joint variation, 

                   V ∝ `\frac{nT}P` (when all parameters vary)

               Or, V = R `\frac{nT}P` [R = universal gas constant]

               Or, PV = nRT --------(1)

Eq. (1) is known as the ideal gas equation.

  

36) How can the molecular mass of gas be determined from the ideal gas equation?

Or, how can we determine the molecular mass of a gas from the equation PV = nRT.

Ans〉We know that the ideal gas equation for n mole of gas is

                                      PV = nRT ----------(1)

where P = pressure, V = volume, T = temperature 

Now, if  weight of gas = W g ＆ molar mass of gas = M g `mol^-1` then n = `\frac WM`.

Then from equation (1) we get-------

                            PV = `\frac WM`RT

                      Or, PM = `\frac WV`RT

                      Or, PM = dRT [∵density, d = `\frac WV`]

                      Or, M = `\frac{dRT}P`

37) What do you mean by molar gas constant or universal gas constant? Why is 'R' called universal gas constant?

Ans〉Molar Gas Constant or Universal Gas Constant: In the case of 1-mole gas, the ratio of the product of pressure and volume of the gas to the absolute temperature is always constant. This constant is called molar gas constant or universal gas constant.

≻ The value of R is equal for 1 gram mole of all ideal gases. Its value does not depend on the nature of the gas. Hence R is called universal gas constant.

38) Calculate the dimension and unit of R.

Ans〉We know that the ideal gas equation for n mole of gas is

                    PV = nRT

ஃ R = `\frac{PV}{nT}`

ஃ Dimensional formula of R 

      dimension of P `times` dimension of V

 = ----------------------------------------------------

  dimension of mole n `times` dimension of T

= `\frac{ML^{-1}T^{-2}\times L^3}{mol\times K}`

= `ML^{2}T^{-2}mol^-1 K^-1`

≻ Unit of universal gas constant R

From dimensional analysis we know that the dimension of R

   = `ML^{2}T^{-2}mol^-1 K^-1`

   = dimension of work `mol^-1 K^-1`

Therefore, unit of R in SI is J `mol^-1 K^-1` and unit of R in CGS is erg `mol^-1 K^-1`.

39) Write the value of molar gas constant R.

Ans〉R = 8.314 J `mol^-1 K^-1`

                = 8.314 `times` `10^7` erg `mol^-1 K^-1`

                = 0.082 L atm `mol^-1 K^-1`

                = 1.987 cal `mol^-1 K^-1` 

40) Write down the postulates of the kinetic theory of gas.

Ans〉The postulates of the kinetic theory of gas are ----

1) All the gases are composed of many molecules. Molecules of the same gas are of same nature but molecules of different gases are of different nature.

2) The gas molecules are solid, spherical and elastic.

3) The gas molecules are always in a motion. This motion is completely random.

8) The total volume of gas molecules is negligible compared to the volume of the vessel.

5) There is no repulsive or attractive force between the gas molecules.

6) As the gas molecules are elastic, the total momentum and kinetic energy of the molecules before and after collision remain unchanged.

6) Gas molecules have no potential energy. The entire energy is kinetic energy.

6) The average kinetic energy of gas molecules is proportional to the absolute temperature of the gas.

41) Write the reasons for the deviation of real gases from the ideal behavior.

Ans〉The two reasons for the deviation of real gases from the ideal behavior are -

1) The finite volume of the molecule of real gas: Although the size of a molecule of real gas is small, each molecule has a certain volume. Therefore, the total volume of the gas molecules relative to the volume of the gas vessel cannot be ignored.

2) The intramolecular force of attraction: The molecules of real gas attract each other. For this attraction force, the value of the pressure exerted by the gas on the wall of the vessel is somewhat lower.